Economy of Efficiency Demystified

Look at every appliance, any technology, and many vehicles sold new today, and you’ll hear all sorts of claims about how more efficient that new thing is compared to its older versions. With those claims of better efficiency, you sometimes hear that the new technology will “pay for itself over time.” What does that mean, and how do we calculate that?

Something paying for itself over time is going to “Break Even,” at the “Break-Even Point.” That is when a purchase.You may hear that in business, but this is slightly modified in concept to apply to more everyday purchases.Refrigerators, dish washers, water heaters, and many more appliances usually have the yearly operating cost on a sticker on the appliance itself, making it very easy to calculate the break-even point.

Economy-efficient

Image courtesy:  https://www.pexels.com/

For example, let us say that a water heater currently installed in a house has a yearly running cost of $650 a year,and that the owners are thinking about replacing it with a newer, more efficient hybrid water heater that will cost $500 a year to use. The new one costs $1,650 dollars to buy and install, and the old one can be sold for $150. To solve it, we set the yearly running costs equal to each other, and add on the costs.650 x = 500 x + 1650 - 150,   650 x = 500 x + 1500,  150 x = 1500,  x =10

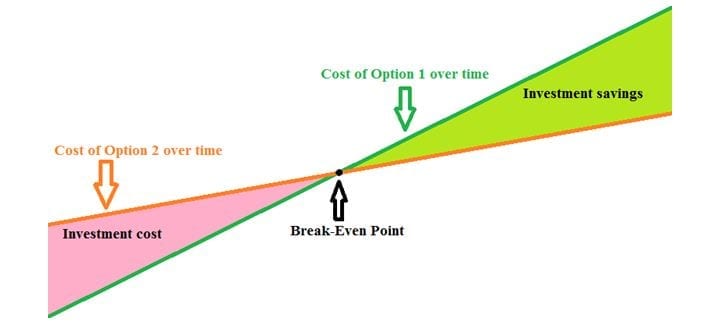
cost-option

Image courtesy:  https://www.pexels.com/

It would take ten years for the new hybrid water heater to pay itself off, compared to keeping the old one, as long as old one doesn’t break or need maintenance. There are other variables out in the real world, like sales, coupons, and other discounts that could bring down that initial cost and help it pay for itself faster, but overall, this is quite a simple example.A more complicated example could be considering a new car. Finding the break-even point when you must calculate the yearly running costs yourself is far more difficult. Let us say someone has a generic 20-year-old sedan and is thinking of downsizing and replacing it with a newer, smaller, and more efficient car. It’s been averaging 20mpg, their insurance averages$1,250 a year, and the maintenance currently averages $300 a year, and increases by 10% every year.

Buying a new car would cost $21,000, but selling the old car would give back $3,000, fuel economy will increase to 27mpg average, and that warranty will pay for enough maintenance to average $100 a year for the rest of its life. However, insurance will increase to $1,500 a year. Assume that fuel will cost $2.75 a year on average, and that you will average 15,000 miles a year in both. To solve it, we need to take all the many factors and make functions that we can set equal to each other.

  • Old sedan: 15,000 miles per year ÷ 20 miles per gallon = 750 gallons per year, 750 gallons per year 2.75 dollars per gallon = 2062.5 dollars per year.
  • Compound interest formula:  A=  P  ( 1 + r/n  )nt,300  ( 1 + 0.1/1  )1x, 300  ( 1.1  )x,
  • The Old Sedan Function: 1,250+2,062.5x=  300( 1.1 )x,3,312.5 x + 300 (  1.1  )x,
  • New hatchback:  15,000 miles per year ÷ 27 miles per gallon = 555.5 ̅ gallons per year, 555.5 ̅ gallons per year × 2.75 dollars per gallon = 1527.7 ̅dollars per year.
  • The New Hatchback Function: 21,000 – 3000 + 1,500x + 1527.7x + 100x, 18,000 + 3,127.7x3,312.5x + 300 ( 1.1 )x = 18,000 + 3,127.7x, 300 ( 1.1 )x + 184.8x = 18,000, 0.616x+ ( 1.1 )x =60
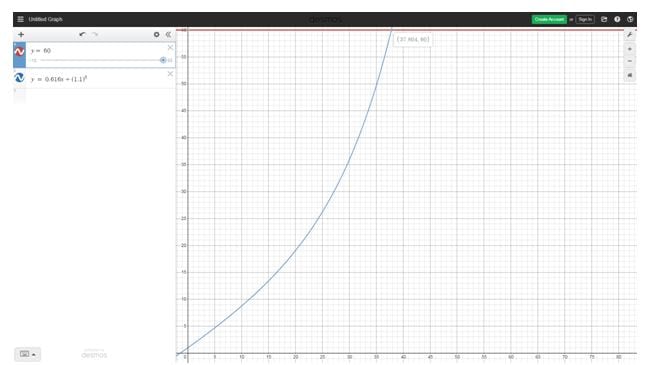
Economy-graph

Image courtesy:  https://www.pexels.com/

This is a very difficult logarithmic function, so unless you are in advanced trigonometry, you have two options. Use an online equation calculator, or an online graphing website. Graphing is much simpler and shown here as y = 60 and y = 0.616x+ ( 1.1 )x and the x-intercept is our desired solution, 37.8 years.Naturally, a new car will have a much better chance at lasting 38 years than one already 20 years old. It will also be safer, more comfortable, produce cleaner emissions, and have more modern amenities. The break-even point in many purchases are beyond  the lifespans of either of their options, costly maintenance aside.

This, however, does not mean that you will never reach it.Often, with some research, you can find ways around purchases that will help you come off better in the long run.

old-sedan

About the author: Mr. Robert Wich teaches math, science and reading at FPLA. He is fascinated by math concepts and wants to share his knowledge with eager learners. His students have shown tremendous progress in their math skills. Currently, he is pursuing mechanical engineering degree at FIU. 

Full Potential Learning Academy (FPLA) is Miami’s premier tutoring center in Reading, Math, Science, and Test Preparation programs. 

At FPLA, we encourage your child to aspire to a bright future by empowering them with academic and life skills in a positive learning environment that is equipped with a variety of learning resources. Thanks to our state-of-the-art online platform you can learn from our expert tutors one-on-one from the comfort of your home. This live One-on-One program ensures stability, dependability, and consistency in the quality of student tutor interactions. 

complicated

Call 305-826-1896 for a free consultation and schedule a demo of our live one-on-one online session.

FPLA tutors:

Our tutors are not just experts in their subjects, but expert tutors as well! Test prep tutors are graduates or college students who took the tests recently. All our tutors have undergone a rigorous selection process, were extensively trained, and continually apply the best tutoring practices to ensure that your child gets the best chance at academic improvement.

For more details call us at 305-826-1896 or explore us at https://www.fullpotentialtutor.com/math-course-assistance/