How To Define Equation of a Line?

By Robert O

The equation of a straight line has the standard form

    \[y=m x+c\]

Where:

  • m is how steep (gradient) the line is. The value can either be negative or positive, but never 0.
  • C is the value of y when x=0 or the y-intercept.
  • If m=1 and c=0, then the line coincides with the x-axis.

The values of x and y just tell us how far along and how far up the line is, respectively.

How do we find an equation of a line given if we have two points?

You can come up with a question of a straight line if you know any two points on the line. You can get these points on a line if given a graph of the line. In some situations, an examiner can state these points for you. In this tutorial, we will use points and finally learn how to read the points from a graph.

In general, if you have two points A(x1, y1) and B(x2, y2), then you can get the equation of a straight line passing through A and B by following these steps.

First, find the value of m using the two points.

    \[m=\frac{\text { change in } y}{\text { change in } x}=\frac{y 2-y 1}{x 2-x 1}\]

Next, choose another arbitrary point on the line, say N(x, y). Using the value of m any point, either A or B, we form the equation of the line.

In general.

    \[m=\frac{\text { change in } y}{\text { change in } x}=\frac{y 2-y 1}{x 2-x 1}=\frac{y-y 1}{x-x 1}\]

That information is enough to make us form an equation of a straight line. Let’s use a few examples to illustrate that.

Example 1:

What is the equation of a line defined by these points (3,4) and (1,1).

Solution

We start by calculating the value of m:

    \[m=\frac{\text { change in } y}{\text { change in } x}=\frac{4-1}{3-1}=\frac{3}{2}\]

Choose an arbitral third point (x, y):

    \[\frac{3}{2}=\frac{y-1}{x-1}\]

By performing cross-multiplication:

    \[3(x-1)=2(y-1)\]

    \[3 x-3=2 y-2\]

    \[3 x=2 y+1\]

Express the result in the form y = m x+c:

    \[y=\frac{3}{2} x-\frac{1}{2}\]

Example 2:

What is the equation of a line defined by the point (3,-2) and a gradient of 4.

Solution

This problem is easier to solve because we don’t have to calculate the gradient. From the statement, m=4. We go straight to choosing an arbitrary point and use the value of m to find the equation of this line.

    \[4=\frac{y-(-2)}{x-3}\]

    \[4=\frac{y+2}{x-3}\]

    \[y+2=4 x-12\]

    \[y=4 x-14\]

How do I compute an equation of a line from a graph?

If you have a graph, pick any two points on the line and get the respective coordinates. Use them to calculate the gradient (slope). The rest of the steps do not change.

Example 3:

Derive the equation of a line from the graph below:

 

 

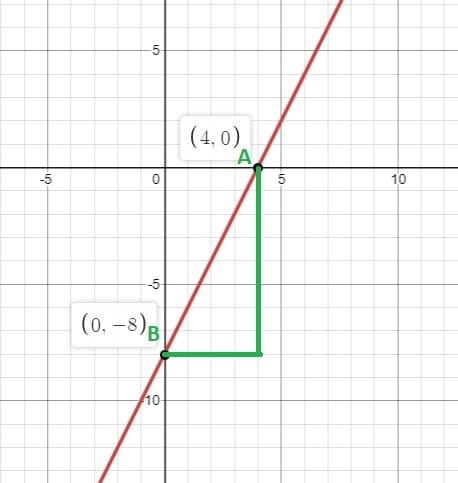
Solution

We pick two points, A and B, on the line and find the respective coordinates. From the graph, A(4,0) and B(0,-8). Remember that you can choose any points, not necessarily A and B.

    \[m=\frac{0-(-8)}{4-0}=2\]

We now use the value of m to find the equation of the line.

    \[2=\frac{y-0}{x-4}\]

Cross-multiplication results in:

    \[y=2 x-8\]

Note:

The value of m will tell you how sloppy or hilly the line is. A negative gradient (m<0) means the line slopes downwards. A positive value (m>0) means you are moving uphill.

Remarks

It is easy to find the equation of a line using coordinates or graphs. Just remember to first calculate the value of m, which is the gradient or slope of the line. Using its value and a third arbitrary point, you can get the equation of that line.

About the Author

This lesson was prepared by Robert O. He holds a Bachelor of Engineering (B.Eng.) degree in Electrical and electronics engineering. He is a career teacher and headed the department of languages and assumed various leadership roles. He writes for Full Potential Learning Academy.