How To Solve Two Linear Equations?

By Robert O

A system of two linear equations (aka simultaneous equation) takes the following form:

    \[a x+b y=m\]

    \[c x+d y=n\]

An equation is linear only if the exponents of the unknown variables equal to one. For a system of linear equations, an equation should have at least one variable.

What are the methods for solving a system of two linear equations?

We will use two methods that are most common among different scholars. The first one is the Gaussian elimination, and the second one is direct substitution.

How to use the Gaussian elimination?

We will demonstrate this using a few examples.

Example 1:

Solve for the values of x and y in

    \[2 x+y=5\]

    \[-x+y=2\]

Solution

To solve these equations using the eliminations method, look at the coefficient of both x and y in the two equations. Find the easier one to eliminate by either adding them together or subtracting one from the other. You can start with any coefficient, but this approach is to make your work easier.

From our equations, it is easier to eliminate y by subtracting the two equations.

    \[\frac{\left.\begin{array}{l}2 x+y=5 \\-x+y=2\end{array}\right]}{3 x=3} \text { subtract }\]

After subtraction, we can easily see that x=1

Using this value of x in any of the equations, we can find y.

    \[2(1)+y=5\]

    \[y=3\]

Solution: y = 3 and x = 1

Example 2:

Solve for values of x and y in:

    \[x-2 y=-2\]

    \[7 x-3 y=19\]

Solution

We make one of the coefficients the same for both of the equations to find the solution. There is no rule on the one to eliminate first. In this case, I prefer eliminating x first by multiplying the first equation by 7 and the second one by 1 and then subtracting.

    \[\begin{array}{l}(x-2 y=-2) \times 7 \\(7 x-3 y=19) \times 1 \\\left.\begin{array}{l}7 x-14 y=-14 \\7 x-3 y=19\end{array}\right] \text { subtract } \\\hline-11 y=-33\end{array}\]

After subtraction, we can see that y = 3.

Substituting y in the original equation, we can find the value of x.

    \[x-2(3)=-2\]

    \[x=-2+6\]

    \[x=4\]

Solution: y = 3 and x = 4

Example 3:

Solve for the values of x and y in:

    \[5 x-4 y=20\]

    \[2 x+1=3 y\]

Solution

The second equation is not in the standard form. We must first convert it.

    \[5 x-3 y=20\]

    \[2 x-3 y=-1\]

We can eliminate x by multiplying the top equation by 2 and the bottom equation by 5.

    \[\left.\begin{array}{l}(5 x-3 y=20) \times 2 \\(2 x-3 y=-1) \times 5 \\\hline \begin{array}{l}10 x-6 y=40 \\10 x-15 y=-5\end{array} \\\hline 9 y=45\end{array}\right]-\text { Subtract }\]

The variable y = 5. Substituting this in any of the above equations, we get:

    \[2 x-3(5)=-1\]

    \[2 x=14\]

    \[x=7\]

Solution: y = 5 and x = 7

How to solve a system of two linear equations using the direct substitution method?

We are going to use example 1 to demonstrate how we can find the solution using direct substitution.

Example 1:

Solve for the values of x and y in

    \[2 x+y=5\]

    \[-x+y=2\]

Solution

Take any of the equations and make one variable the subject. I will use the first equation (there is no criterion for doing this).

    \[2 x+y=5\]

    \[y=5-2 x\]

Next, we substitute this value for y in the second equation to have only one unknown in x.

    \[-x+(5-2 x)=2\]

    \[-x+5-2 x=2\]

    \[-3 x=-3\]

    \[x=1\]

Substitute x = 1 in any of the equations and find that y = 3. These are the exact solutions from example 1 using the Gaussian elimination method.

How to solve simultaneous equations using graphical method?

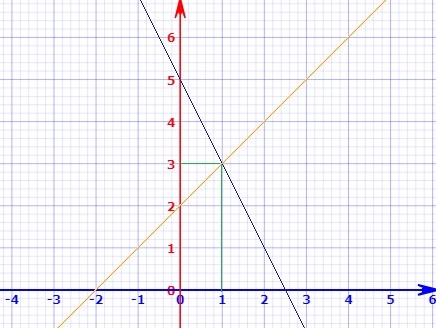
We can also find solutions to two linear equations using graphs. To do that, we calculate two points for each equation to help us in plotting.

For equation -x + y = 2, we construct a table. When y = 0, x = – 2 and when x = 0, y = 2.

    \[\begin{array}{|l|l|l|}\hline y & 0 & 2 \\\hline x & -2 & 0 \\\hline\end{array}\]

For the second equation 2x + y = 5, we can also construct a table.

    \[\begin{array}{|l|l|l|}\hline y & 0 & 5 \\\hline x & 2.5 & 0 \\\hline\end{array}\]

Using these values to plot the graphs, we get two intersecting lines. The point of intersection gives the solution. Read the values of x and y on the x-axis and y-axis, respectively. We find that x = 1 and y = 3.For the second equation 2x + y = 5, we can also construct a table.

Note:

A system of two linear equations has no solution if they are parallel. How do you know that they are parallel without plotting the lines on graph paper? It is simple! Just express the equations in the form y = m x + c where m is the gradient of the lines. If the value of m in both equations is the same, then there is no solution.

A system of two linear equations has infinitely many solutions if the two equations have the same slope.

Remarks

Regardless of the approach, you will always find the solution if the equations do not have the same gradient (slope). By regular practice, you should become your own master in solving linear equations. The knowledge is helpful in solving for variables in systems with two or more linear equations.

About the Author

This lesson was prepared by Robert O. He holds a Bachelor of Engineering (B.Eng.) degree in Electrical and electronics engineering. He is a career teacher and headed the department of languages and assumed various leadership roles. He writes for Full Potential Learning Academy.

    \[\begin{array}{|l|l|l|} \hline y & 0 & 5 \\ \hline x & 2.5 & 0 \\ \hline \end{array}\]