Distance, Time, Speed, and Acceleration

Where are we going? And how are we getting there? How fast are we going there? How can we change that? Where did I leave my keys? In this article, we’ll answer the first four questions. The final question is too difficult for anyone to figure out. I’ll probably stumble upon them soon.

Distance is the measurement between one point and another point in space. It is directionless, so it cannot be negative. However, displacement is distance following a direction, which can be negative. For now, we will assume that distance is linear, always shown as a straight line, as it is in basic mathematics. The advanced mathematics required for curved lines are unnecessary for the following relationships between distance and time. The most common units of distance are the inch, foot, yard, mile, centimeter, meter, and kilometer.
Time is a linear construct depicting moments of passing. We usually use it to determine how long it takes something to happen. It is seemingly abstract but no less very important and is applied to our lives daily. We determine time in seconds, minutes, hours, etc.
Now we can play with mathematics. What happens when we want to find out how much distance we cover over a period of time? Simple! We divide our distance by the amount of time spent going that distance. If it takes us 40 seconds to cover 80 feet, we simply set up a fraction like this: and simplify the problem to , or 2 feet per second (2). This is what we know as speed. Dividing any distance by any time gives us our speed. Meters per second, miles per hour, and kilometers per hour are the most commonly used units of speed.

Since speed has no direction, it cannot be negative. However, Velocity is speed with a direction, and that is when it can be negative. We also must eliminate a remainder in the denominator. If the numbers do not divide evenly (such as 21 miles per 5 hours), we must divide our distance by our time to get a decimal (which, in this case, would be 4.2 miles per hour.)
We can have even more fun with mathematics if we put in some extra time. What if we ran at 2 feet per second for one second, and then 4 feet per second for the next second, and then 6 feet per second the second after that, and keep increasing our speed at this rate? This is where we square (what we call multiplying something by itself) time. If we start from a speed of zero, and increase our speed by 2 feet per second every second, we are experiencing acceleration of 2 feet per second per second, or 2 feet per second squared, or 2ft /second2 .
Since acceleration is how fast we are speeding up, it can be negative. Negative acceleration is called deceleration, and it is how fast we are slowing down.2
Since acceleration is squared, we must keep the units of time the same. It is incorrect to say that we are accelerating at 2 feet per minute per second, or 2 feet per second per minute, and we must convert them to have the same unit of time. It is easiest to convert the larger unit of time to match the smaller unit of time. 2 feet per 60 seconds per second is 0.0 feet per second, and 2 feet per second per minute is 2 feet per second per 60 seconds, or 120 feet per second. This is shown here algebraically:

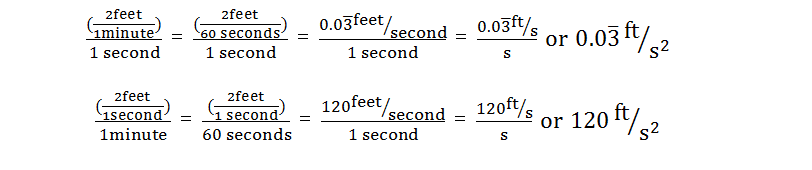
We experience these physics daily in our everyday lives as we move our own bodies and objects around them. You experience speed even when sitting still, from the earth’s own speed in space! You accelerated and decelerated your fingers when you typed or wrote today. You accelerated and decelerated your own pupils as your eyes moved from one point to another on this very article on acceleration! Movement is speed and where there is speed, there is or was acceleration. And now you know the basics of how to find the speed and acceleration of anything you see!
About the author:
Mr. Robert Wich teaches math, science and reading at FPLA. He is fascinated by math concepts and wants to share his knowledge with eager learners. His students have shown tremendous progress in their math skills. Currently, he is pursuing mechanical engineering degree at FIU.
