How to Write Equation of a Perpendicular Line

By Robert O

Two perpendicular lines form an angle of 90o at the intersection point. That is, they make 90o at the intersection point. To know that a line is perpendicular to another line, check its gradients or slopes.

How do I know if line A is perpendicular to line B?

If the equation of line A is

    \[y=m 1 x+c\]

and that of line B is

    \[y=m 2 x+c\]

then line A is perpendicular to line B if and only if:

    \[m 1 \times m 2=-1\]

You can get the equation of a second line that is perpendicular to the first line if you have the equation of the first line and one point of the second line. Let’s see that by solving some example problems.

Example 1

What is the equation of a line that passes through a point (2, 4), and is perpendicular to another line whose equation is

    \[y-2=4 x\]

Solution

Rewriting the equation in the standard form

    \[y=m x+c\]

    \[y=4 x+2\]

We can easily tell that the gradient of the first line, m1 = 4.

Using the formula

    \[m 1 \times m 2=-1\]

we can get the gradient of a second line that is perpendicular to the first one.

    \[m 1 \times m 2=-1\]

    \[4 \times m 2=-1\]

    \[m 2=-\frac{1}{4}\]

The second point of the line is (2, 4). We take the third point on the line (x, y) and apply the formula

    \[m=\frac{\text { change in } y}{\text { change in } x}=\frac{y 2-y 1}{x 2-x 1}=\frac{y-y 1}{x-x 1}\]

    \[-\frac{1}{4}=\frac{y-4}{x-2}\]

Cross-multiplication results into:

    \[4 y-16=-x+2\]

    \[4 y=-x+18\]

    \[y=-\frac{1}{4} x+4.5\]

The graph below shows the two lines. The red line represents the equation

    \[y=-\frac{1}{4} x+4.5\]

and the green line represents the equation y-2 = 4 x We can see that they meet at right angles (perpendicular).

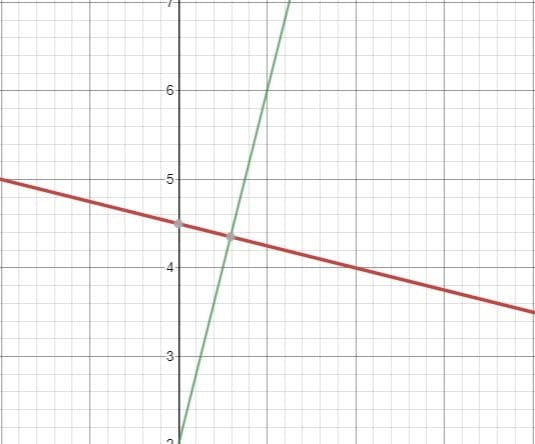
Graph generated from https://www.desmos.com/

Example 2:

Find the equation of another line perpendicular to a line whose equation is y= 2 x+4 and passes through the point (1, 1) on a Cartesian plane?

Solution

We can readily see that m 1=2. Let’s calculate m2:

    \[m 1 \times m 2=-1\]

    \[2 \times m 2=-1\]

    \[m 2=-\frac{1}{2}\]

We apply the formula as follows:

    \[m=\frac{\text { change in } y}{\text { change in } x}=\frac{y 2-y 1}{x 2-x 1}=\frac{y-y 1}{x-x 1}\]

    \[-\frac{1}{2}=\frac{y-1}{x-1}\]

    \[2 y-2=-x+1\]

    \[y=-\frac{1}{2} x+1.5\]

Let’s graph the two equations to see if they are perpendicular.

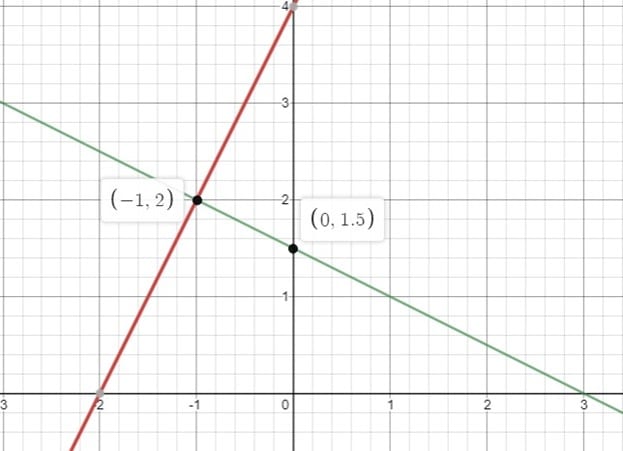
Graph generated from https://www.desmos.com/

Remarks

If you know the gradient of one line or you have its equation, then it is easy to find the equation of another line that is perpendicular to it. You only need to know at least one set of coordinates of a point on that line. It is a straightforward calculation using the fact that the product of gradients of two perpendicular lines is always -1 .

About the Author

This lesson was prepared by Robert O. He holds a Bachelor of Engineering (B.Eng.) degree in Electrical and electronics engineering. He is a career teacher and headed the department of languages and assumed various leadership roles. He writes for Full Potential Learning Academy.