Triangles for SAT Prep

Last updated on
by Arikaran Kumar

Share0
Tweet0
Share0
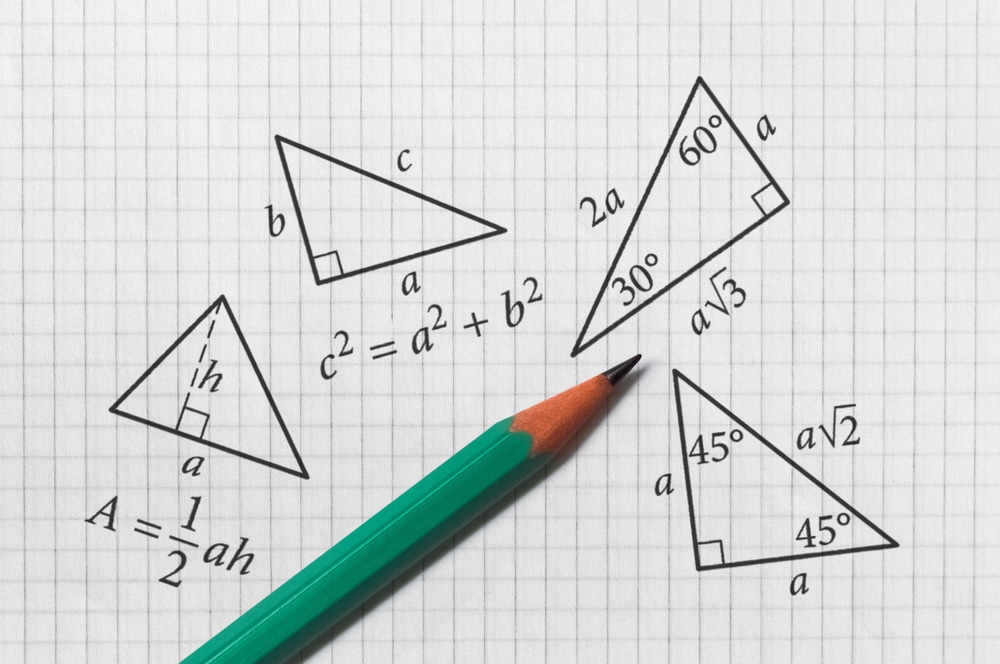
Triangles for SAT Prep

What is a triangle? 

(Go To Table Of Contents)

  • A triangle is a type of polygon that has three sides and three angles.
  • The sum of the interior angles of a triangle MUST equal $180^{\circ}$.
  • The sum of the exterior angles of a triangle MUST equal $360^{\circ}$.
  • The area of a triangle is A=\frac{1}{2} b h, where A is area, b is the base and h is the height.
  • The base can be any side of the triangle.
  • The height (altitude) of the triangle is a line perpendicular to the base and starts from the angle opposite to the base. (When two intersecting lines are perpendicular, they form $90^{\circ}$ angles notated by the ∟ symbol.)
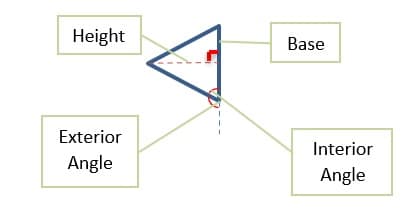
Figure 1

Figure #1

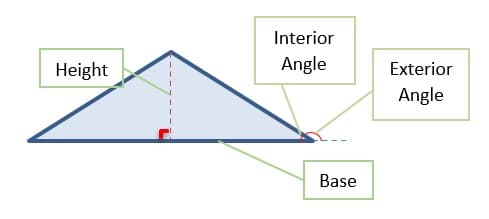
Figure 2


Figure #2

Now that we have discussed some properties of a triangle, let’s apply what we know to some examples.

Examples 

(Go To Table Of Contents)

Find the area of each given triangle.

#1

Question 1

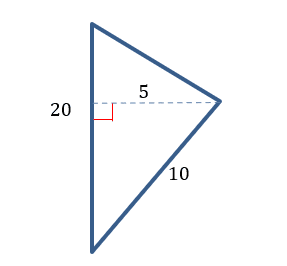
Figure #3

Remember:  

The area of a triangle is A=\frac{1}{2} b h. 

The base, b, can be any side of the triangle. The height, h , is a line perpendicular to the chosen base. In Figure #3, we can see that we already have a line perpendicular to one of the sides of the triangle. So, the side that measures 20 will be our base. The line that is perpendicular to our chosen base will be our height, which measures 5.

So, b = 20 & h = 5

Now all we must do is plug each value into our area formula and solve.

A=\frac{1}{2} b h

A=\frac{1}{2}(20)(5)

A=\frac{1}{2} \times 100=50

The area of this triangle is 50 square units.

Side Note: 

The side with the measure of 10 IS NOT the height. It is possible for it to be a base for us to select, but we would also need a line to be perpendicular to the given side. Since there is no line perpendicular to this side, we can’t use it as our base. 

#2

Question 2

Figure #4

In Figure #4, the base is 100 and the line perpendicular to the base measures 24.

So, b = 100 & h = 24

A=\frac{1}{2} b h

A=\frac{1}{2}(100)(24)

A=\frac{1}{2} \times 2400=1200

The area of this triangle is 1200 square units.

We Make Math Learning Fun! 

(Go To Table Of Contents)

Mastering an equation a day makes you smarter everyday. For those who need that extra help to learn math concepts, FPLA certified tutors offer 1-on-1 tutoring.

FPLA Math tutoring program includes:

Evaluation test

Regular feedback

Customize tutoring plan

Algebra, Geometry, Calculus, Trigonometry and more

Qualified instructor lead, live, online 1-on-1 tutoring

Affordable

Evaluation test

Qualified instructor lead, live, online 1-on-1 tutoring

Algebra, Geometry, Calculus, Trigonometry and more

Customize tutoring plan

Regular feedback

Affordable

Find the missing angle, x, of each given triangle.

#3

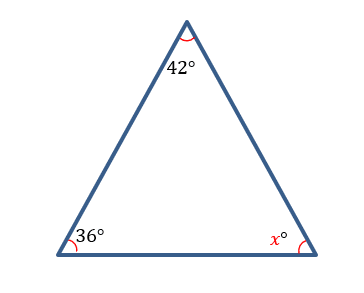
Find the missing angle, x ,of each given triangle.

Figure #5

Remember:  

The sum of the interior angles of a triangle MUST equal $180^{\circ}$. 

To find  x  Figure #5, we can make the following equation:

42^{\circ}+36^{\circ}+x^{\circ}=180^{\circ}

Simplifying, we get

42^{\circ}+36^{\circ}+x^{\circ}=180^{\circ}

78^{\circ}+x^{\circ}=180^{\circ}

Next, we can isolate x by subtracting 78^{\circ} from both sides.

78^{\circ}+x^{\circ}-78^{\circ}=180^{\circ}-78^{\circ}

x^{\circ}=102^{\circ}

Book a Free Consultation Now!

To Learn more about Trigonometry tutoring at FPLA schedule an appointment with us!

 Book Now !Free. Schedule A Call.

#4

Question 4

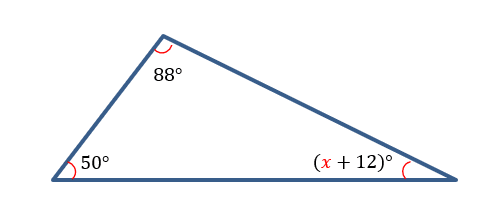
Figure #6

For Figure #6, we need to create an equation to solve for x. Since the sum of the interior angles is 180^{\circ}, we can write:

50^{\circ}+88^{\circ}+(x+12)^{\circ}=180^{\circ}

Which can be rewritten as

50^{\circ}+88^{\circ}+x^{\circ}+12^{\circ}=180^{\circ}

Simplifying, we get

50^{\circ}+88^{\circ}+x^{\circ}+12^{\circ}=180^{\circ}

x^{\circ}+150^{\circ}=180^{\circ}

Subtracting 150^{\circ} from both sides we get

x^{\circ}+150^{\circ}-150^{\circ}=180^{\circ}-150^{\circ}

x^{\circ}=30^{\circ}

Author: Mr. Vernon Sullivan, is a tutor at FPLA Miami, FL HQ premier 1-on-1 tutoring center. He teaches Algebra, Geometry, Pre-Cal, ACT, SAT, SSAT, HSPT, PERT, ASVAB and other test prep programs.

Ms. E.R. Suryalakshmi proofread this article. Mr. Arikaran Kumar manages the website and the social media outreach.

Critical Skills That You Need to Cultivate in College
Critical Skills That You Need to Cultivate in College Although there are hundreds of different subjects to study and majors[...]
Read More 
How to Kill Time Without Killing Others?
Social distancing: How to Kill Time Without Killing Others?Under the quarantine, our whole species has been advised, if not ordered,[...]
Read More