Right Triangles Demystified

Last updated on J by Arikaran Kumar

Share0
Tweet0
Share0
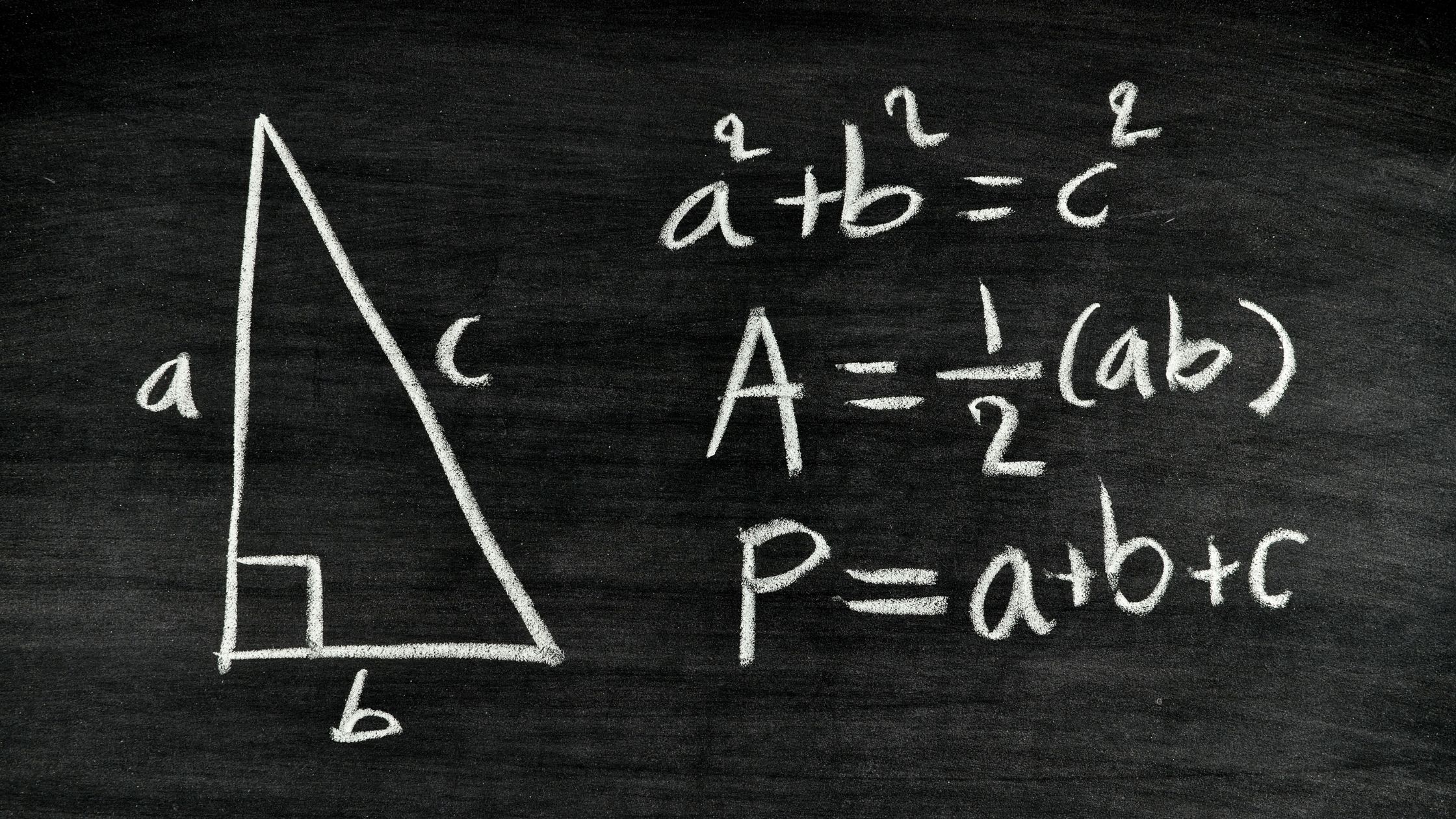
Right Triangles

Right Triangles

What is a Right Triangle? 

(Go to the Table Of Contents)

A right triangle is a special type of triangle in which one of the angles measures $90^{\circ}$. When we do have a right triangle, the measure of the remaining two angles that are not the right angle CANNOT be equal to 90^{\circ}, as the sum of all interior angles of a triangle must be equal to $180^{\circ}$. A $90^{\circ}$ angle is usually notated by the ∟ symbol. Here are some examples:

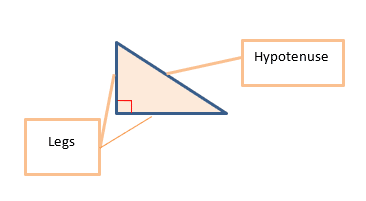
Figure 1

Figure #1

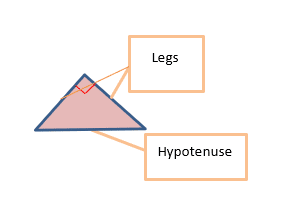
Figure 2

Figure #2

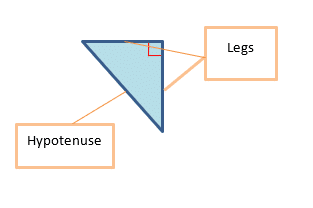
Figure #3

In each of these triangles, the $90^{\circ}$ angle is located where the ∟ symbol is.

BONUS TIP:  

In a right triangle, the longest side is known as the hypotenuse. The hypotenuse will ALWAYS be the side opposite of the $90^{\circ}$ angle. (Since the largest angle in a Right Triangle is always $90^{\circ}$ and the longest side is always opposite the largest interior angle). The two shorter sides are known as legs.

What is a special right triangle? 

(Go to the Table Of Contents)

Now that we know about right triangles, let’s talk about two special types of right triangles. Each triangle will have either of the following measures for its three angles.

$30^{\circ}$ - $60^{\circ}$ - $90^{\circ}$     OR     $45^{\circ}$ - $45^{\circ}$ - $90^{\circ}$ 

30° – 60° – 90° 

(Go to the Table Of Contents)

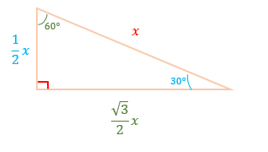
In a $30^{\circ}$ - $60^{\circ}$ - $90^{\circ}$ right triangle, one angle measures   $30^{\circ}$, one angle measures $60^{\circ}$, and one angle measures $90^{\circ}$. The sides of the triangle opposite to each angle have a ratio of \frac{1}{2}:\frac{\sqrt 3}{2}:1, respectively.

  • The side opposite to $30^{\circ}$ is equal to \frac{1}{2}x 
  • The side opposite to $60^{\circ}$ is equal to \frac{\sqrt 3}{2}x
  • The side opposite to $90^{\circ}$ is equal to x
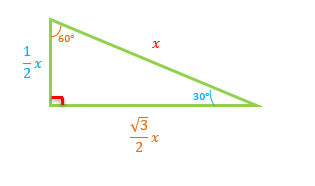
Figure 4

Figure #4

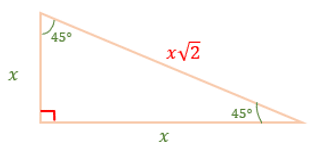
45° – 45° – 90° 

(Go to the Table Of Contents)

In a $45^{\circ}$ - $45^{\circ}$ - $90^{\circ}$ right triangle, one angle measures   $90^{\circ}$ and two angles measure $45^{\circ}$. The sides of the triangle opposite to each angle have a ratio of 1:1:\sqrt 2.

  • The sides opposite to each $45^{\circ}$ angle is equal to x
  • The side opposite to $90^{\circ}$ is equal to x\sqrt 2
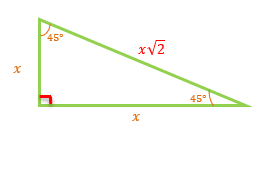
figure 5

Figure #5

Using these properties, we can easily solve for the remaining sides of a right triangle if given only one side measurement and knowing that we have a special right triangle.

Fun facts about right triangles: 

(Go to the Table Of Contents)

  • Right triangle has many synonyms. Right-angled triangle, orthogonal triangle, rectangled triangle; the common thread, a triangle having one of the angles measuring 90^{\circ}.
  • The foundations of trigonometry can be traced to the study of the relationship between the sides and the angles, other than the 90^{\circ}, of a right triangle.

Book a Free Consultation Now!

To Learn more about Trigonometry tutoring at FPLA schedule a free consultation.

 Book Now !Free. Schedule A Call.

Examples 

(Go to  the Table Of Contents)

Find the missing side,z, of each given triangle.

#1

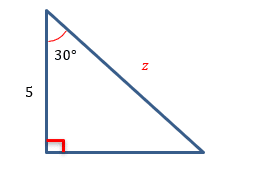
Figure 6

Figure #6

For the problem in Figure #6, we are only given one side of the triangle. To solve for the missing side, z, let’s first solve for the remaining angle. We can do that by setting up the following equation:

90^{\circ}+30^{\circ}+p^{\circ}=180^{\circ}

Where p is the value of the missing angle.

Figure 6 (1)

Simplifying we get

90^{\circ}+30^{\circ}+p^{\circ}=180^{\circ}

120^{\circ}+p^{\circ}=180^{\circ}

Solving for p we get

120^{\circ}+p^{\circ}-120^{\circ}=180^{\circ}-120^{\circ}

p^{\circ}=60^{\circ}

Since p^{\circ}=60^{\circ}, we can see that we have a $30^{\circ}$ - $60^{\circ}$ - $90^{\circ}$ triangle. Using this information, we can solve for the missing side z.

Figure 6 (2)

The side we are given is opposite of 60^{\circ}. The side opposite of 60^{\circ} is equal to \frac{\sqrt 3}{2}x. Therefore,

5=\frac{\sqrt 3}{2}x

Solving for x we get

(\frac{2}{\sqrt 3})5=\frac{\sqrt 3}{2}x(\frac{2}{\sqrt 3})

\frac{10}{\sqrt 3}=x

Rationalizing we get

(\frac{\sqrt 3}{\sqrt 3})\frac{10}{\sqrt 3}}= x

\frac {10 \sqrt 3}{3}=x

The side z is equal to x. So,

z=x

z=\frac {10\sqrt 3}{3}

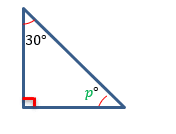
#2

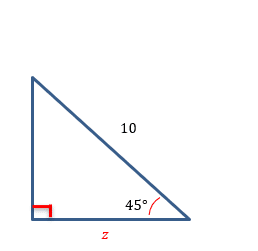
figure 7

Figure #7

In Figure #7, we will once again begin with solving for the missing angle. We’ll call it g. So,

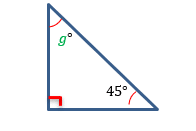
Figure 7 (1)

90^{\circ}+45^{\circ}+g^{\circ}=180^{\circ}

135^{\circ}+g^{\circ}=180^{\circ}

Solving for p we get

135^{\circ}+g^{\circ}-135^{\circ}=180^{\circ}-135^{\circ}

g^{\circ}=45^{\circ}

Since g^{\circ}=45^{\circ}, we can see that we have a $45^{\circ}$ - $45^{\circ}$ - $90^{\circ}$ triangle. Using this information, we can solve for the missing side z.

Figure 7 (2)

The side we are given is opposite of 90^{\circ}. The side opposite of 90^{\circ} is equal to x \sqrt 2. Therefore,

x \sqrt 2=10

Solving for x we get

\frac {x \sqrt 2}{\sqrt 2}=\frac {10}{\sqrt 2}

x=\frac {10}{\sqrt 2}

Rationalizing, we get

x=\frac {10}{\sqrt 2}(\frac {\sqrt 2}{\sqrt 2})

x=\frac {10 \sqrt 2}{2}

Simplifying, we get

x= 5 \sqrt 2

The side z is equal to x. So,

z=x

z=5 \sqrt 2

Author: Mr. Vernon Sullivan, is a tutor at FPLA, a premier 1-on-1 tutoring center HQ in Miami FL. He teaches Algebra, Geometry, Pre-Cal, ACT, SAT, SSAT, HSPT, PERT, ASVAB and other test prep programs.

Mrs. Emimmal Sekar Proofread this article. Mr. Arikaran Kumar manages the website and the social media outreach.

Step by Step 4 HS years
Step by Step Approach to Space Out And Prepare for the SAT/ACT® Tests Through Your HS Years Freshman Discuss your career[...]
Read More 
Using The Laws Of Logarithms To Solve The Equation
[Latexpage]How To Solve Logarithmic Equations with Log Laws?By Robert OIn a previous lesson, you learnt how to find logarithmic base.[...]
Read More